L’académie de Grenoble propose une progression et une banque d’énoncés de problèmes pour chaque niveau du cycle 2 et pour le CM1-CM2. Cette banque de problèmes a été construite par Marie Gehard et les PEMF de l’Isère à partir du travail et des recommandations de Sophie Thuillier, CPD Maths et du groupe départemental mathématiques de l’Isère.
Chaque progression s’appuie sur la typologie des problèmes de Vergnaud (1986) car elle est connue
des enseignants. L’objectif est d’identifier les difficultés en jeu dans la résolution des problèmes
additifs/soustractifs et multiplicatifs/de division.
Les énoncés ont été pensés afin de véhiculer le moins possible de stéréotypes, de représenter la diversité culturelle (choix des prénoms rencontrés dans les classes, prénoms de diverses origines).
Afin que les enfants mis en scène dans les énoncés ne soient pas cantonnés à des activités dites « de
garçons » pour les garçons et « de filles » pour les filles, un certain nombre d’énoncés sont modifiés. Pour les mêmes raisons, les énoncés qui concernent les activités et les métiers attribués
aux adultes, sont modifiés en octroyant indifféremment aux femmes et aux hommes des activités et métiers généralement attribués aux uns ou aux autres : infirmiers, caissiers, femmes pompier, présidente de la République, conductrice de camion…
L’aspect langagier est réfléchi afin d’utiliser des verbes plus précis que le verbe « faire ». L’utilisation de la première personne est évitée car il pourrait être source de confusion pour les élèves fragiles de CP.
Pour éviter que les élèves ne s’enferment dans l’exécution d’une procédure sans réflexion, les types de problèmes sont diversifiés dans une même semaine.
Comme certains élèves, rapides et performants, ont besoin d’être confrontés à des problèmes plus difficiles, chaque semaine, il y a des « problèmes + » (pour « plus difficiles »)
Chaque semaine sont donc proposés dix problèmes du même type, quatre « problèmes + », quatre problèmes d’autres types, et quatre « problèmes + » d’autres types, soit au total, vingt-deux problèmes.
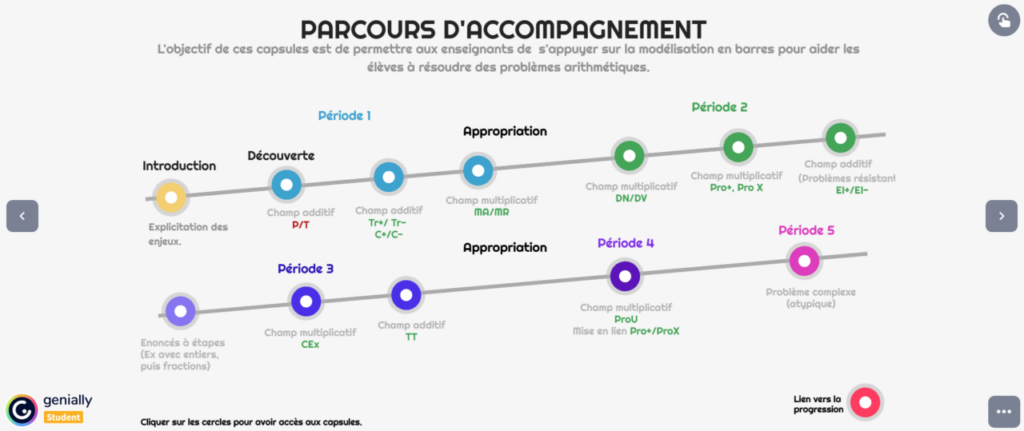
En CM1 et CM2, des capsules vidéo accompagnent les enseignants pour s’appuyer sur la modélisation en barres pour aider les élèves à résoudre des problèmes.
–
Pour en savoir plus, vous pouvez lire cet article de la COPIRELEM et consulter les nombreux documents sur le site de l’académie de Grenoble : https://mathematiques38.web.ac-grenoble.fr/resolution-de-probleme